I was reading Peter Pesic's Abel's Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability when I came across the story of Adriaan van Roomen and Francois Viète. The former, a Dutch mathematician, had in 1593 put out a challenge problem to the mathematicians of all the world:
The Dutch ambassador to the court of Henri IV ironically suggested to the French king that there was no mathematician in his kingdom who could solve this equation. Henri summoned Viète. Viète was already a well-known cryptographer and mathematician, he had recently published a book on trigonometric formulae, and - fortunately for la gloire de France - recognised the equation as an expansion of some powers of trigonometric functions. In a few minutes he was able to determine the twenty-three positive solutions of van Roomen's problem, and the following day he provided the remaining 22 negative solutions as well (although he disdained them).
Van Roomen was extremely impressed, travelled to Paris, met Viète, and they remained buddies for the rest of their lives. Aww, you might say. Geek man-crush and all that.
Looking at this equation, I have no idea where to begin solving it. Descartes' rule of signs tells me that there are twenty-three sign changes in the equation, indicating the existence 23 positive roots (not all necessarily distinct, of course). By the fundamental theorem of algebra, we know that an algebraic equation in the 45th power will have forty-five roots. So we can deduce that there will be 22 negative roots. But what the devil are they?
Recourse to the programming environment R's polynom package is easily done, but as that's a numerical solver, the nested square roots in the constant part of the above equation can create instabilities rendering the final answer somewhat unlikely. Indeed, I find that I get a bunch of complex roots, whereas Viète determined real-valued solutions.
I thought I might use Wolfram Alpha to solve the equation symbolically. Unfortunately, the polynomial definition is too long for the input box on that site.
Another problem is that there appear to be different versions written down of the equation: some of the coefficients are different (e.g. I've seen 740,259x35 and 740,459x35; there are other discrepancies as well.)
Perhaps I should use the clue that Viète used a trigonometric identity to solve the equation. By the sixteenth century, several of these were already known in Europe. For example,
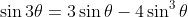
If we let
, we can get a cubic equation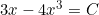 
, where 
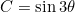. Were a solver to recognise the left-hand-side as an expansion for a trigonometric function, he or she would be able to use the identity to solve the algebraic equation. Similarly, Viète realised that using the above substitution for x, that large 45th degree equation reduced to 
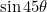, which he could then solve using a table of sines.1
If we let
Check out Philippe Henry's paper (in French)2 - it's got as comprehensive a treatment of the problem and Viète's approaches to solving it as you might want. I gotta tell you - it has less to do with algebra than geometry. And indeed, the reason Viète rejected the negative solutions is that they did not make sense in 'real life'. Or, that is to say, geometry.
References
1. Jeff Suzuki, Mathematics in Historical Context, page 189.
2. Philippe P. A. Henry, La solution de François Viète au problème d’Adriaan van Roomen, 2008.
0 comments:
Post a Comment