JOST A MON: A Theorem

Nov 11, 2012

A Theorem

It's been a while since I've CodeCogged, and I'm pleased to find that the site is still there. This brings out an intemperate desire to see some fancy mathematical typesetting, and an email from Springer provides the impetus. I get free previews for the occasional paper, you see, and it's always fun to look at its contents and realise, once again, that while I might understand every word in a sentence, I have no idea what the thing in its entirety means.

So, anyway, here's a theorem from Alexander Kuznetsov (2008) 'Lefschetz decompositions and categorical resolutions of singularities', Selecta Mathematica (New Series), Volume 13, Number 4, pp 661-696.

Theorem 1. The triangulated category $\widetilde{D}$ with functors $\pi_{*}$ and $\pi^{*}$ is a categorical resolution of $D^{b}\left ( Y \right )$ . Moreover, we have a semiorthogonal decomposition

$D^{b}\left ( \widetilde{Y} \right )=\left \langle i_{\bullet} \left \left ( B_{m-1} \otimes L^{1-m} \right )\right,\left ( B_{m-2} \otimes L^{2-m} \right ), \cdots ,\left ( B_{1} \otimes L^{-1} \right ),\widetilde{D}\right \rangle.$

Finally, if $Y$ is Gorenstein and $K_{\widetilde{Y}}=\pi^{*}K_{Y}+\left ( m-1 \right )\widetilde{Z}$ then

$\widetilde{D}$ is weakly crepant if $p^{*}\left ( D^{perf}\left ( Z \right ) \right )\subset B_{m-1},$

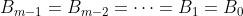
$\widetilde{D}$ is strongly crepant if $B_{m-1}= B_{m-2}=\cdots=B_{1}=B_{0}$

Kuznetsov goes on to say: 'Certainly, minimal categorical resolutions are the most interesting.'

One day I'll figure out how to inline the LaTeX so that it doesn't appear off the rest of the text. Good thing to have an occasional challenge, eh?

JOST A MON

The idle ramblings of a Jack of some trades, Master of none

A Theorem

0 comments:

Post a Comment

Links

About Me

Categories-