I have often wondered why it was that the same Pythagorean proof for the irrationality of the square root of 2 was inflicted on students. Surely there were other proofs? The Wikipedia article on this shows three in all: the usual one, a slight variant, and a geometric construction.
Recently, though, I came across another one 1. It is also based on reduction ad absurdum, i.e., a proof by contradiction. It is due to T. Estermann (1902 - 1991), who claimed it to be the first new proof since Pythagoras.
First, establish the fact that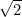 exceeds
exceeds 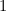 .
.
This is not difficult, as you can show that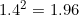 and
and 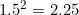 , and so
, and so 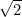 lies between
lies between 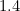 and
and 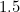 .
.
Clearly, then, the square root of 2 is not a whole number.
Consider the set S of all positive integers n such that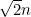 is also an integer.
is also an integer.
Now, if S is not empty, then it has a least member. Why is that? Because any non-empty set of integers can be sorted in ascending order, and will therefore have a least element. Let this element be k. Then it follows that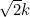 is an integer.
is an integer.
Construct the numberk) .
.
What can we say about u?
1. u is smaller than k
2. u is positive, and it is an integer because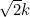 is an integer, subtracting k from which results in yet another integer.
is an integer, subtracting k from which results in yet another integer.
3. Because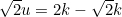 , we have that
, we have that 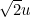 is also a positive integer.
is also a positive integer.
Therefore:
4. u is a member of S.
But this is a contradiction! We had that k was the smallest element of S, and now we have shown that u, which is smaller than k is also a member of S.
So our assumption that S is non-empty is false. In other words, S is empty.
In which case there is no positive integer n such that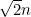 is also an integer.
is also an integer.
Therefore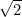 is not a fraction.
is not a fraction.
In other words, it is irrational.
Oooo, sir, as one might say.
Reference
1. J. Derbyshire, Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics
Recently, though, I came across another one 1. It is also based on reduction ad absurdum, i.e., a proof by contradiction. It is due to T. Estermann (1902 - 1991), who claimed it to be the first new proof since Pythagoras.
First, establish the fact that
This is not difficult, as you can show that
Clearly, then, the square root of 2 is not a whole number.
Consider the set S of all positive integers n such that
Now, if S is not empty, then it has a least member. Why is that? Because any non-empty set of integers can be sorted in ascending order, and will therefore have a least element. Let this element be k. Then it follows that
Construct the number
What can we say about u?
1. u is smaller than k
2. u is positive, and it is an integer because
3. Because
Therefore:
4. u is a member of S.
But this is a contradiction! We had that k was the smallest element of S, and now we have shown that u, which is smaller than k is also a member of S.
So our assumption that S is non-empty is false. In other words, S is empty.
In which case there is no positive integer n such that
Therefore
In other words, it is irrational.
Oooo, sir, as one might say.
Reference
1. J. Derbyshire, Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics

2 comments:
Isn't "any non-empty set of integers can be sorted in ascending order" another equivalent of the axiom of choice? Thus making this proof not very 'set theoretic' in the ZF sense?? This, together with the use of Peano's axioms as used in the proof would make it amenable to disagreements at an esoteric level :-p Just an observation... I agree with the proof though!
Hiya V! Good to hear from you. This is hardly a set-theoretic proof, is it? It's difficult enough to define numbers in set theory; operations such as square root are much worse. Don't remember much about ZF and axiom of choice, so can't comment on the equivalence you ask about. :-)
Post a Comment